Computed tomography (CT) enables visualization of the internal structure of an object without cutting it open. This is extremely useful and finds extensive applications in medicine, for instance, to observe the changes in the internal anatomy. It is also used to visualize the internal structure of plant specimens, as well as in the fault detection of fabricated objects in the manufacturing sector. While it is true that there is no explicit physical damage, CT does require passing a uniform beam of X-rays through an object from multiple directions as shown below.
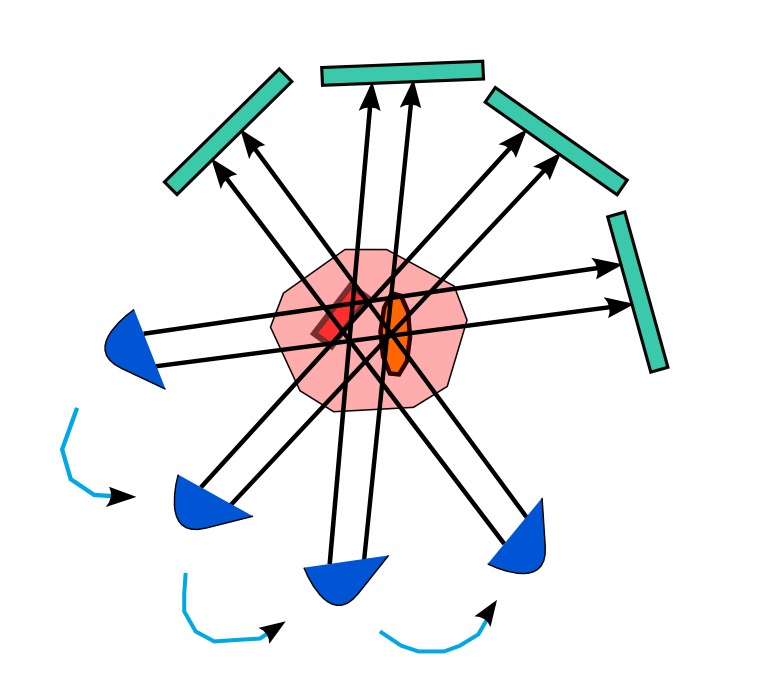
Differences in the local absorption of the X-rays convey information about the internal object density variations. High intensity X-rays sent from a large number of directions -- theoretically infinite -- enables excellent clarity of the internals. However, reducing the exposure to these rays has always been sought after in order to prevent the specimen from damage, especially if it is being imaged multiple times over an extended time duration. For this reason, one may either
- reduce the number of directions along which rays are passed (few-view), or
- reduce the intensity (low-dose) of rays
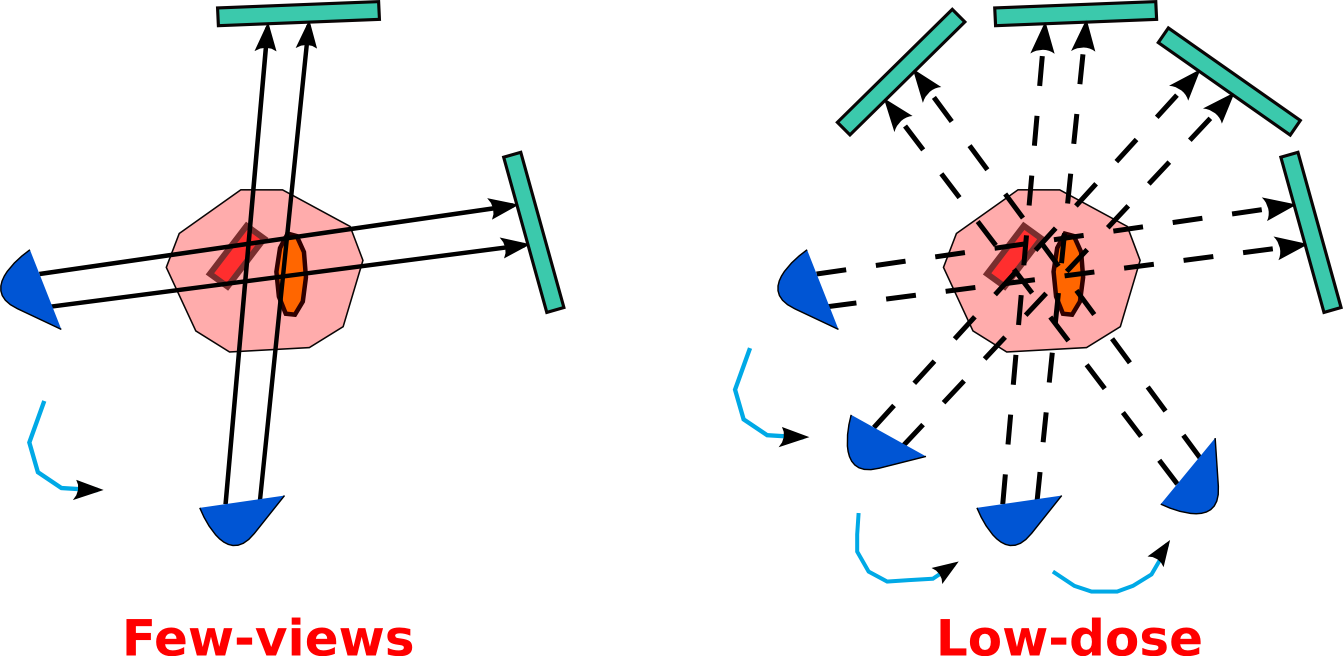
The figure below shows the kind of artefacts that appear when reconstructing from few-view and low-dose measurements.

This thesis aims to reduce the above artefacts by using data-driven (prior-based) techniques within the widely used Compressed Sensing (CS) framework, for each of the above scenarios: few-view imaging and low-dose imaging. We specifically focus on reconstructing in longitudinal studies i.e., when repeated scans of an object are taken to study the changes within it over a period of time.
Problem Statements
- Given no information about the object, reconstruct from its few-view or low-dose measurements, with minimal artefacts.
- Given previous high quality scans of similar or identical objects, reconstruct the current object (`test') from its few-view or low-dose measurements, with minimal artefacts.
- An intrinsic danger in using prior is its dominance in the reconstruction, which leads to inaccurate reconstruction of new changes in the test that were not present earlier. This defeats the very purpose of longitudinal studies. Hence, one of our goals is to ensure that the reconstructions of new changes in the test is not biased by the prior.
The figure below gives an outline of where our work fits in within the imaging and reconstruction pipeline.
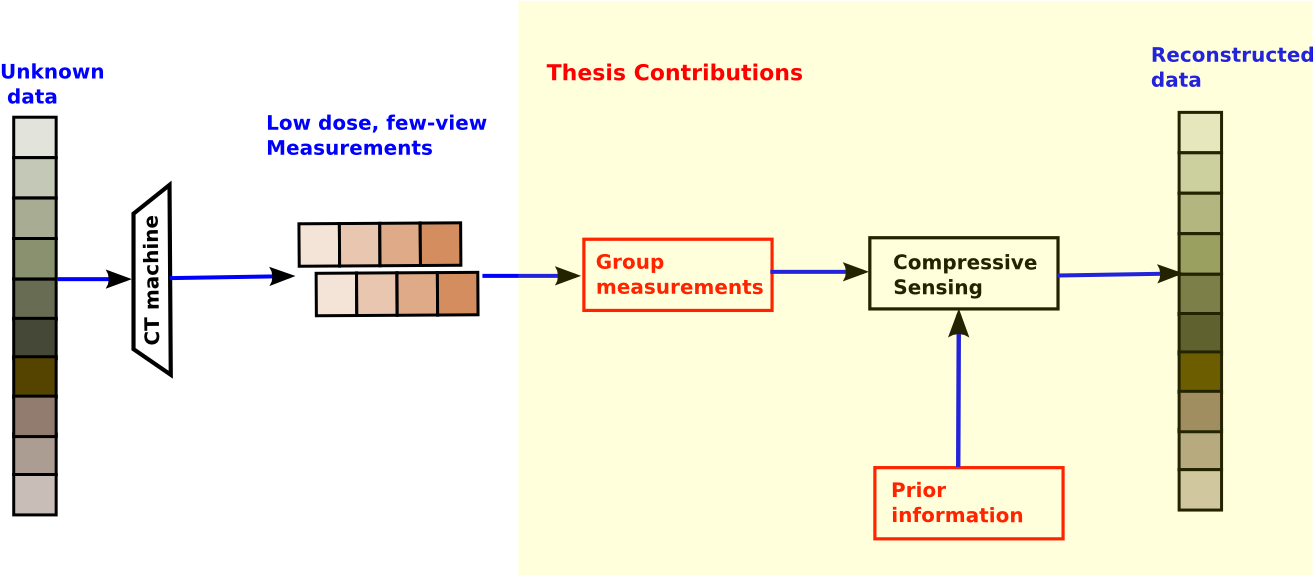
In conventional data acquisition techniques, measurements are acquired by sampling the physical object uniformly above the Nyquist rate. In few-view imaging, the measurements are taken from an exceedingly small number of views; however, these are with standard strength X-rays, i.e., the intensity of each beam is kept to current practices. We discuss the reduction of artefacts in few-view imaging under the following two scenarios:
Reconstruction With Prior
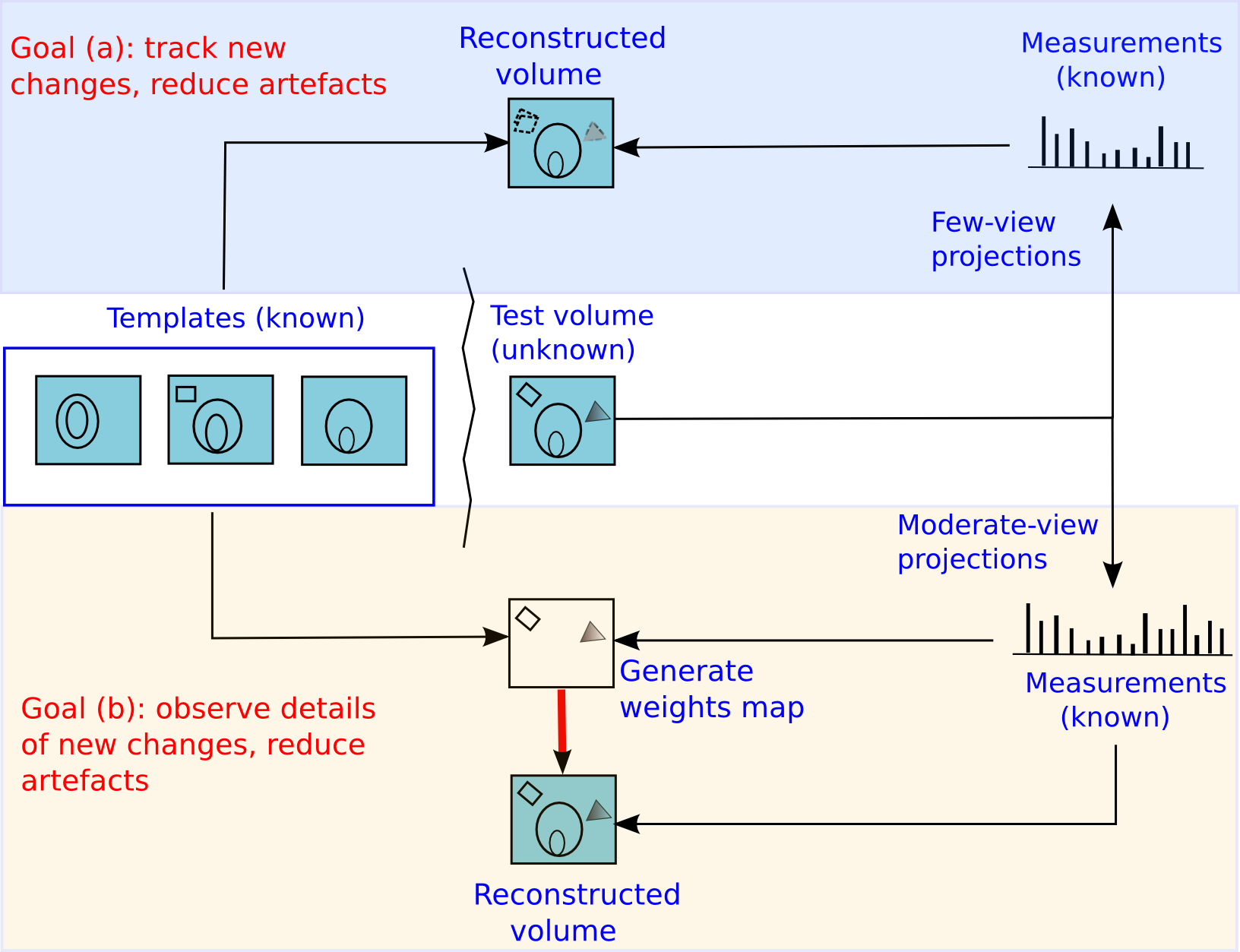
We deal with the case of longitudinal studies, wherein an object is imaged multiple times to observe the changes it undergoes over a period of time. Given previous good quality scans of an object ('templates'), we reconstruct the current data ('test') from its few-view measurements.
An overview of our method is shown below. The choice of the number of measurement views and the type of reconstruction is driven by the goal in any application. When our goal is simple-- to track the location of new changes while simultaneously reducing sub-sampling artefacts, we propose to (a) capture measurements from few views ('few-view' imaging) and use unweighted prior-based reconstruction. When our goal becomes more ambitious-- to observe details of the new changes while simultaneously reducing sub-sampling artefacts, we propose to (b) capture measurements from a slightly higher number of views (`moderate-view' imaging) and use weighted prior-based reconstruction.
Sample Result: 3D reconstruction
One of our datasets consists of a longitudinal study performed on an okra specimen. Multiple scans were taken, each time after introducing a small incision on one of its sides. We reconstructed one of the volumes ('test') by assuming the other volumes as templates. Since our goal here is to accurately observe the new details (presence or absence of the incision), we observe that the weighted prior method accurately reconstructs the new changes.
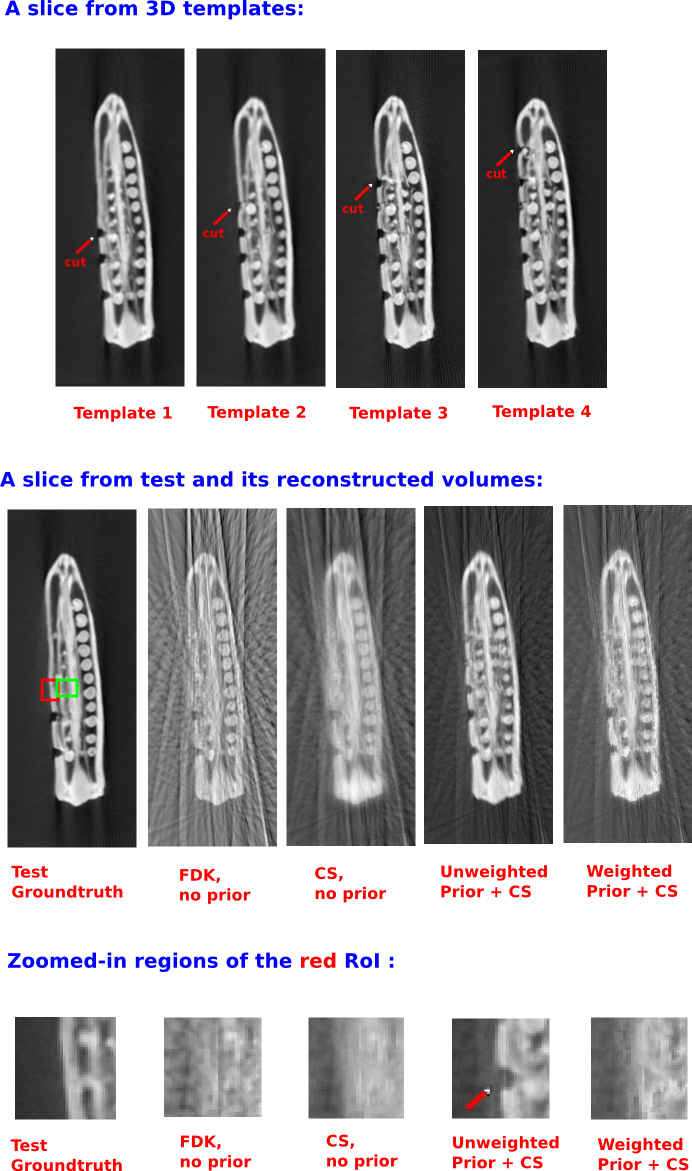
Reconstruction Without Prior
Grouping Measurements
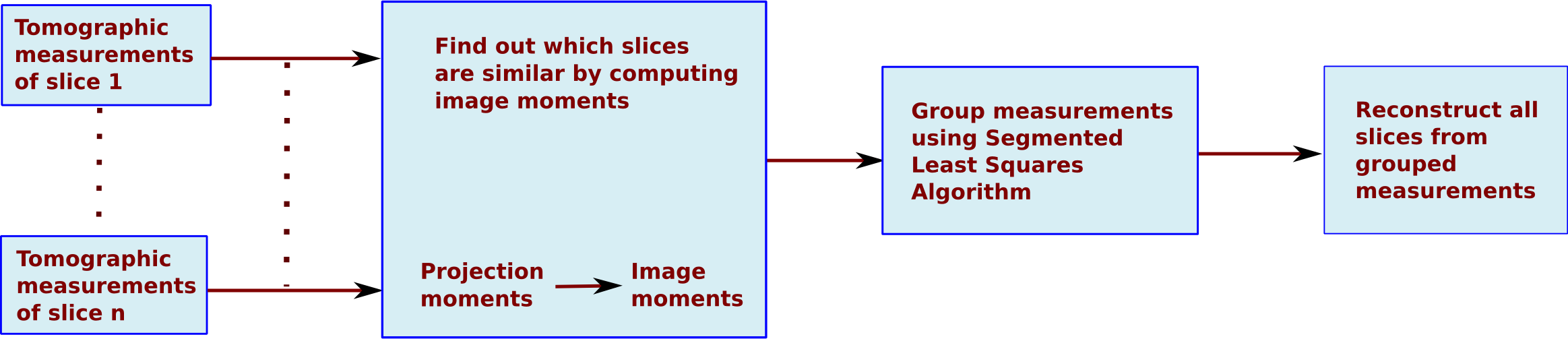
When prior is unavailable, we exploit the inherent redundancy with the data. If the measurements from different views of two similar objects are combined, then we show that the reconstructions of both the objects improve. This is due to the presence of additional information that would have otherwise not been utilized had the two objects been reconstructed from their respective measurements alone. Specifically, within the CS framework, we reconstruct only a reference slice and its difference from the neighbouring similar slices. The difference between two similar slices is sparser than any of the individual slices. This improves the reconstruction within the CS framework.
Challenge: Since the data is unknown to begin with, we do not know which parts of the data are similar and which are not. Hence we first compute the image moments from the Radon projection moments. Similarity in image moments is inferred as similarity between underlying slices. Once the image moments of all slices are computed, their measurements are grouped based on a similarity metric and an optimal grouping mechanism through the Segmented Least Squares Algorithm. The grouped measurements are then reconstructed together, and the others are reconstructed independently. An overview of this algorithm is shown below:
Sample Result: 3D Reconstruction
This video shows the reconstruction of a volume of 60 slices from the Brainweb dataset.
Reconstruction from Partial Fourier Space
In this section, we view tomographic measurements from a different perspective. The central limit theorem relates the tomographic measurements to samples in the Fourier space along the direction of imaging. Hence, sub-sampling in CT directly corresponds to sub-sampling the spectrum of the imaged object. Here, we propose a direct one-step reconstruction technique that can serve as a good initialization for iterative schemes.
In our experiments, we have considered the hypothetical case of being provided with the Fourier spectrum of a 2D image sampled by Costas autocorrelation sequence. Our aim is to predict the remaining Fourier samples and hence be able to reconstruct the image. We start with a raw estimate of the spatial reconstructed image. We then apply a series of morphological filters on this image with varying sizes of structuring elements (SE). An overview of our technique is shown below:
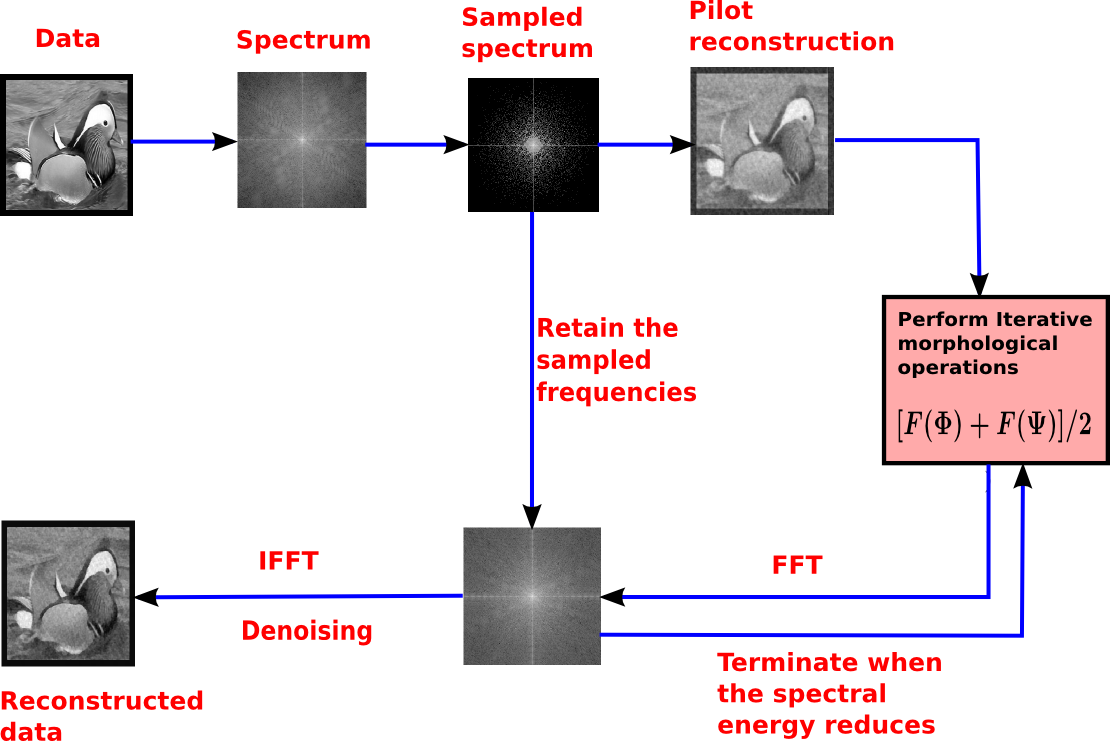
Morphological operations ('opening' and 'closing') have the following advantages:
- The intensity of the 'opened' and 'closed' images are tight bounds on the intensity of the image on which these operations are applied.
- The effect of these operations are seen in just one pass. Further filtering with the same SE does not produce new changes.
Sample Result:
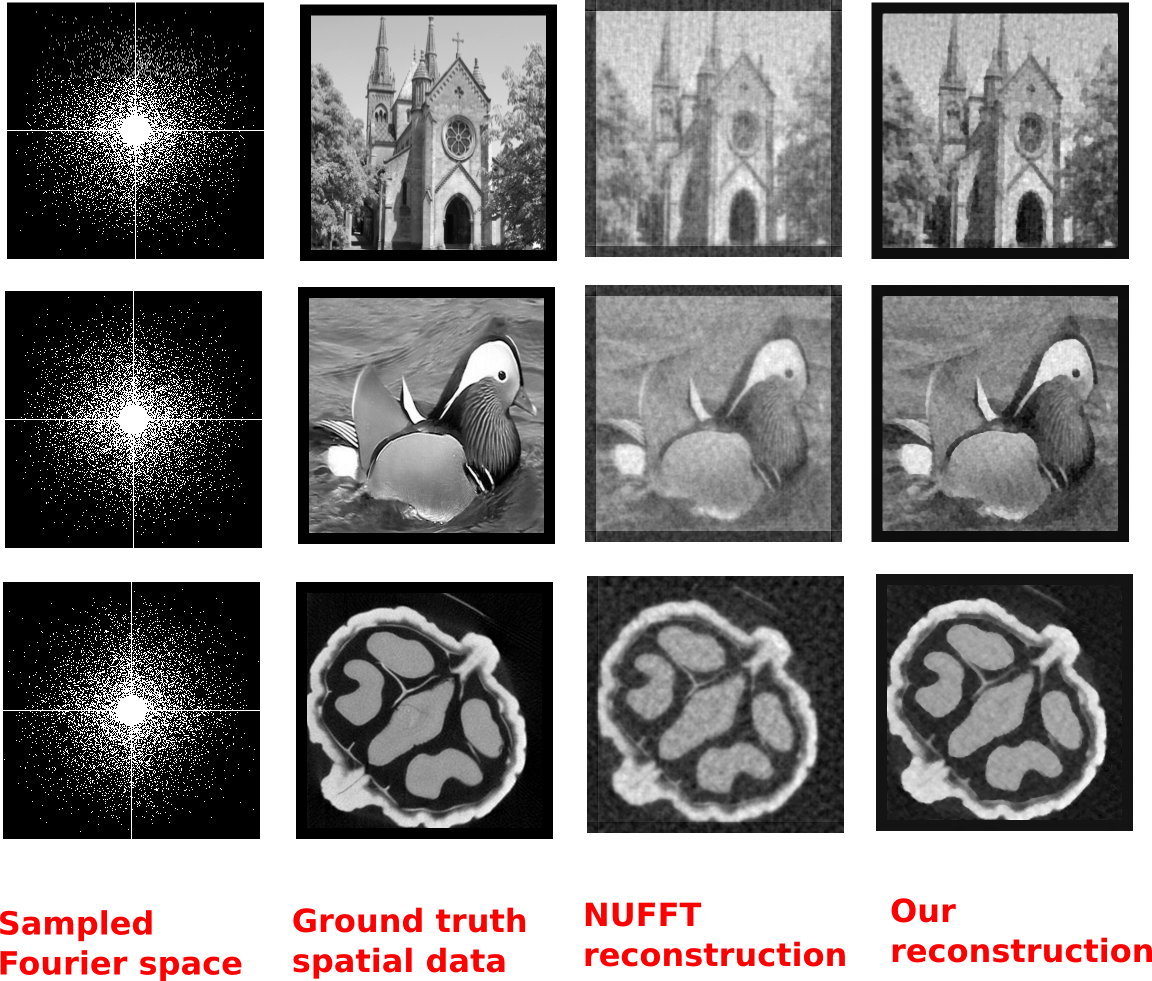
This technique is generic and can be applied to Fourier spectra sampled in any pattern.
Reconstruction With Prior
We deal with the case of longitudinal studies, wherein an object is imaged multiple times to observe the changes it undergoes over a period of time. Given previous good quality scans of an object ('templates'), we reconstruct the current data ('test') from its low-dose measurements. When our goal is to observe the new changes in the test accurately, we apply the weighted prior based technique to detect the location and the intensity of new changes. Once the changes are detected, this information is appropriately used to again enhance the reconstruction with improved sensitivity to changes over any altered regions.
Sample Result: 3D reconstruction
One of our datasets consists of a longitudinal study performed on a potato specimen. Multiple scans were taken, each time after introducing a small incision into the potato. We reconstructed one of the volumes ('test') by assuming the other volumes as templates. Our goal here is to accurately observe the new details i.e., presence or absence of the incision. We see that the weighted prior method accurately locates the new changes and reconstructs it. On the other hand, the unweighted prior dominates the reconstruction and adversely affects the new changes.
Reconstruction Without Prior
If the dose were high, then the post-log methods are good enough. However, they are inadequate for low-dose regime. In the presence of Poisson random noise, the imaging model is no longer linear or even deterministic. In such a scenario, there are multiple ways to model the noisy imaging process. In this thesis, we use a new Poisson-Gaussian Convolution Reconstruction (PGCR) method and compare its performance with the following techniques:
- Post-log filtered backprojection (no noise modeling)
- Rescaled non-linear least squares (partial modeling of Poisson noise)
- Negative likelihood Poisson-Gaussian (modeling of Poisson and Gaussian noise)
Sample Result: 2D reconstruction
A quantitative comparison of the above methods was perfomed for varying values of X-ray dose. Results on one of the datasets is shown below.
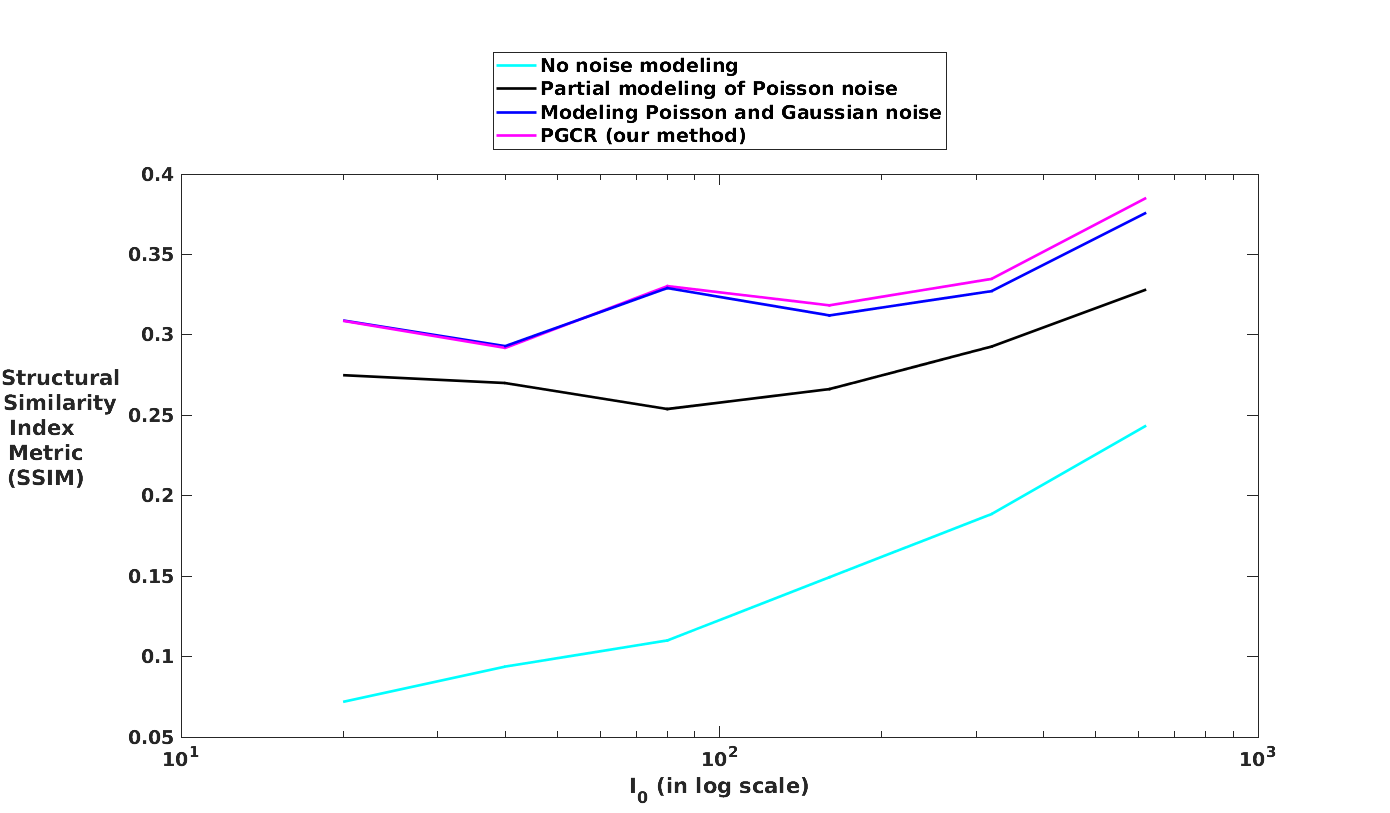
Among the above methods, we choose rescaled non-linear least squares for future reconstructions with prior as this technique offers a good balance between computation time and accuracy.
Journal
- Preeti Gopal, Sharat Chandran, Imants Svalbe and Ajit Rajwade, Low Radiation Tomographic Reconstruction With and Without Template Information , Signal Processing (Elsevier), 2020.
- Preeti Gopal and Imants Svalbe, Spatial domain morphological filtering for interpolation of the Fourier domain, Pattern Recognition Letters, December 2018.
A journal manuscript presenting techniques for reconstruction from few-view measurements is currently under review.
Conferences
- Preeti Gopal, Sharat Chandran, Imants Svalbe and Ajit Rajwade, Low Dose Tomography: Poisson- Gaussian Convolution-based Reconstruction, an abstract, International Symposium on Biomedical Imaging, April 2019.
- Preeti Gopal, Sharat Chandran, Imants Svalbe and Ajit Rajwade, Tomography in Longitudinal Studies: Detecting New Structures from Sparse Measurements, an abstract, International Sympo- sium on Biomedical Imaging, April 2019.
- Preeti Gopal, Ritwick Chaudhry, Sharat Chandran, Imants Svalbe and Ajit Rajwade, Tomographic reconstruction using global statistical priors, Digital Image Computing: Techniques and Applications , December 2017.
- Preeti Gopal, David Bailey and Imants Svalbe, Nonlinear Interpolation in the Fourier Domain Guided by Morphologic Filters, International Conference on Digital Image Computing: Techniques and Ap- plications (DICTA), December 2017.
- Preeti Gopal, Sharat Chandran, Imants Svalbe and Ajit Rajwade, Multi-slice tomographic reconstruction: to couple or not to couple, Indian Conference on Computer Vision, Graphics and Image Processing, December 2016.
- Preeti Gopal, Ajit Rajwade, Sharat Chandran and Imants Svalbe, A Comparison of Some Methods for Direct 2D Reconstruction from Discrete Projected Views, Discrete Geometry for Computer Imagery, April 2016.
